数式解法では，x,yの座標系を設定し，モーメント以外のすべての力をx方向の 力とy方向の力に分解します。 そして，x方向の力をすべて加え合わせて0になる方程式と，y方向の力をすべ て加え合わせて0になる方程式を立てます。 次に，任意の適当な点で，すべての力によるモーメントを計算し，そのモーメント が0になる式を立てます。 以上の3つの式から，反力を計算します。 また，2点のモーメ
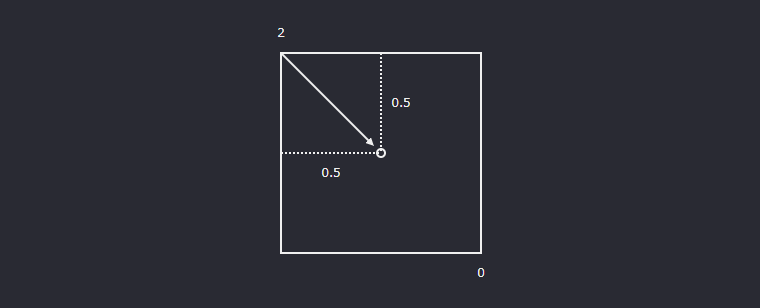
0 真ん中に点-選択したオブジェクトのピボットを中央に戻すには 変換ツールを選択します。 修正 > 中央にピボット ポイントを移動(Modify > Center Pivot)を選択します。 ピボットが、オブジェクトのバウンディング ボックスの中央に移動します。 選択したシェイプのピボットを中央に戻すには 注 センター まず、球の中心点の座標を求めるために、点S・Tの中央に位置する点の座標を求めます。 （2点は直径の両端なので、その 2点の真ん中の座標は球の中心となります ） ST間の中心を点Cとおくと、 この作業で（x4 )2 (y5 )2 (z4 )2=r2 の式のうち、r 2 以外が埋まり、残りの半径rは、空間座標での2点間の距離の公式によって、｜ST｜を求め、 その半分を計算することで求まりま
0 真ん中に点のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  |  |
「0 真ん中に点」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | /post_image_a54ade22-6329-41cc-a229-569d1b96cb79.jpg "どうぶつつなひきのルール インスト By アッサム ボードゲーム情報") |  |
「0 真ん中に点」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「0 真ん中に点」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「0 真ん中に点」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「0 真ん中に点」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「0 真ん中に点」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「0 真ん中に点」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「0 真ん中に点」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
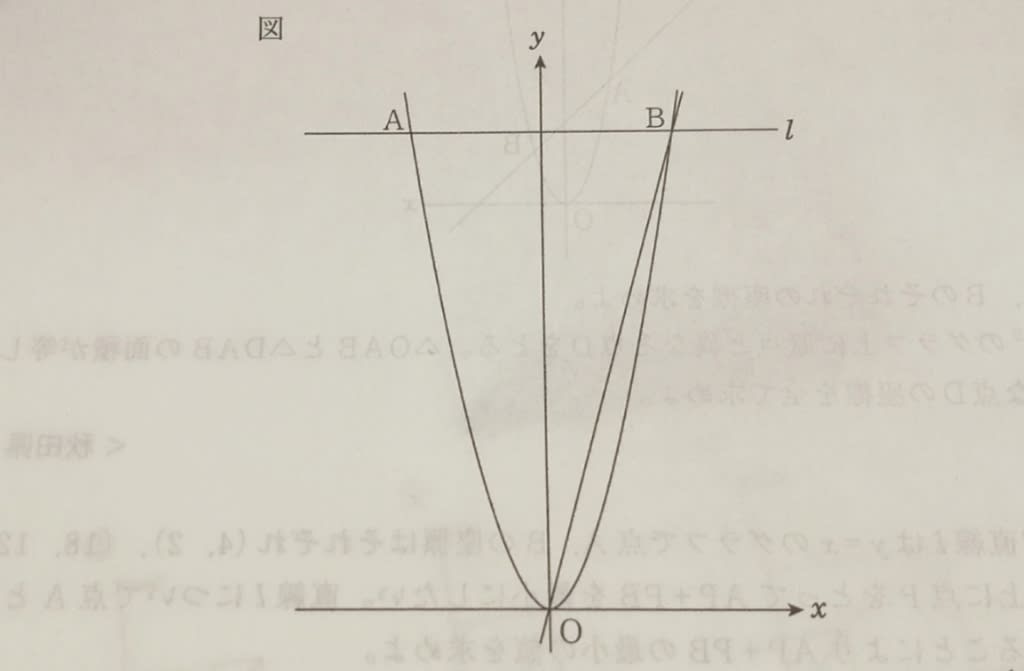
①アクティブ要素 「最後に選択したオブジェクト」がピボットポイントになります。 最後に選択したオブジェクトは、黄色枠で表示されます。 （最後以外のオブジェクトはオレンジ色で表示される） この場合、右のオブジェクトが「最後に選択したオブジェクト」となる。 なので、右のオブジェクトを中心にして回転している。 ②中点 「選択した全てのオブジェクトの中心（中点）」2点 F(, 0) , F'(−, 0) を双曲線の焦点という． 点 A(a , 0) , A'(−a, 0) を頂点という． 2つの焦点の中点を双曲線の中心という．(1)の双曲線の中心は原点 O( 0 , 0 ) にある． (1)の双曲線は x 軸， y 軸，中心に関して対称となっている．
Incoming Term: 0 真ん中に点,
